Algoritmo de Bellman-Ford
O que é o Algoritmo de Bellman-Ford?
O Algoritmo de Bellman-Ford é utilizado para encontrar o caminho mais curto a partir de uma única fonte em um grafo ponderado. Diferentemente do algoritmo de Dijkstra, ele pode lidar com pesos negativos nas arestas.
Origem e História
O algoritmo foi inicialmente proposto por Alfonso Shimbel em 1955. Posteriormente, Richard Bellman e Lester R. Ford Jr. publicaram versões independentes do algoritmo em 1958 e 1956, respectivamente. Em 1959, Edward F. Moore também publicou uma variação do algoritmo, razão pela qual ele é, por vezes, denominado Algoritmo de Bellman-Ford-Moore.
Bellman, conhecido por desenvolver o conceito de programação dinâmica, aplicou essa técnica ao algoritmo, permitindo a resolução de problemas de otimização ao decompor problemas complexos em subproblemas mais simples.
Características
O algoritmo se encaixa nas seguintes categorias:
- Algoritmo de Grafos: Resolve o problema relacionado ao caminho mais curto a partir de uma única fonte.
- Algoritmo de Programação Dinâmica: Utiliza a ideia de subproblemas sobrepostos para calcular a menor distância de um vértice até todos os outros.
Para que serve?
O Algoritmo de Bellman-Ford resolve o problema do caminho mínimo em grafos ponderados, mesmo quando existem pesos negativos. Além disso, ele pode detectar ciclos negativos, tornando-se essencial em diversas aplicações.
Principais aplicações
- Redes de Computadores: Utilizado no Routing Information Protocol (RIP) para calcular rotas mais eficientes.
- Logística e Transporte: Planejamento de trajetos e otimização de custos de transporte.
- Finanças: Modelagem de arbitragem e identificação de inconsistências em taxas de câmbio.
Quando usar?
O Bellman-Ford é a escolha certa quando:
- Pesos negativos estão presentes: Diferente do Dijkstra, ele funciona corretamente mesmo com pesos negativos.
- É necessário detectar ciclos negativos: Importante em cálculos financeiros e redes de fluxo.
- O número de arestas não é muito grande: O algoritmo tem complexidade O(V × E), então é eficiente quando o grafo não é muito denso. Se o grafo não possui pesos negativos e exige uma solução mais rápida, Dijkstra pode ser uma opção melhor.
Bellman-Ford vs. Dijkstra
| Critério | Bellman-Ford | Dijkstra |
|---|---|---|
| Pesos negativos | ✅ Funciona corretamente | ❌ Não funciona |
| Detecção de ciclos negativos | ✅ Sim | ❌ Não |
| Complexidade | O(V × E) |
O(V log V + E) (com heap) |
| Melhor para | Grafos com pesos negativos ou necessidade de detecção de ciclos | Grafos sem pesos negativos, onde rapidez é essencial |
Conclusão: Use Dijkstra para eficiência quando não houver pesos negativos. Escolha Bellman-Ford se precisar lidar com pesos negativos ou detectar ciclos negativos.
Conceitos fundamentais
Antes de entender o funcionamento do Algoritmo de Bellman-Ford, é essencial conhecer alguns conceitos-chave sobre grafos e caminhos mínimos.
Grafos Direcionados e Não-Direcionados
- Um grafo direcionado possui arestas com direção, ou seja, uma conexão A → B não significa que existe B → A.
- Um grafo não-direcionado possui conexões bidirecionais (A ↔ B).
- O Bellman-Ford pode ser aplicado a ambos, mas em grafos não-direcionados com pesos negativos, pode haver ciclos negativos triviais, tornando a solução indefinida.
Pesos nas arestas (Positivos e Negativos)
- Cada aresta em um grafo tem um peso (ou custo), representando distância, tempo, custo financeiro ou qualquer outra métrica que represente o custo de se mover de um vértice para outro. O que chamamos de Grafo Ponderado.
- O Dijkstra falha com pesos negativos, pois assume que encontrar um caminho ótimo mais curto significa apenas somar pesos.
- O Bellman-Ford resolve esse problema, permitindo caminhos mínimos mesmo em grafos com pesos negativos.
O conceito de relaxamento de arestas
- O relaxamento é o processo central do Bellman-Ford. O algoritmo atualiza repetidamente a menor distância conhecida para cada vértice, garantindo que o caminho mínimo seja encontrado ao longo do tempo.
- Se uma aresta (U → V, peso W) puder reduzir a distância para V, a atualização ocorre:
dist(V) = min(dist(V), dist(U) + W)
Detectando ciclos negativos
- Se, após V-1 iterações, ainda houver uma atualização possível, significa que existe um ciclo negativo, ou seja, um caminho em que a soma dos pesos das arestas é negativa.
- Isso causa um problema, pois significaria que o caminho poderia ser sempre reduzido indefinidamente
Funcionamento
Agora que entendemos os conceitos fundamentais, vamos ver como o algoritmo funciona na prática.
- Inicializar Distâncias:
- Definir um vértice de origem S e inicializar todas as distâncias como infinito (∞), exceto o nó de origem, que recebe 0.
- Relaxar Todas as Arestas V−1 Vezes:
- Para cada aresta (u → v, peso w), atualizar a distância para V se encontrar um caminho mais curto via U.
- Repetir esse processo V-1 vezes (onde V é o número de vértices), garantindo que todas as possíveis melhorias sejam feitas.
- Verificar Ciclos Negativos
- Percorrer todas as arestas novamente.
- Se alguma aresta ainda puder ser relaxada, significa que há um ciclo negativo no grafo.
Passo a Passo Teórico
A seguir, apresentamos um exemplo prático da execução do Algoritmo de Bellman-Ford usando um grafo direcionado e ponderado.
graph LR
A -->|4| B
A -->|2| D
B -->|2| C
B -->|3| D
B -->|3| E
D -->|1| B
D -->|6| C
D -->|4| E
E -->|-5| C
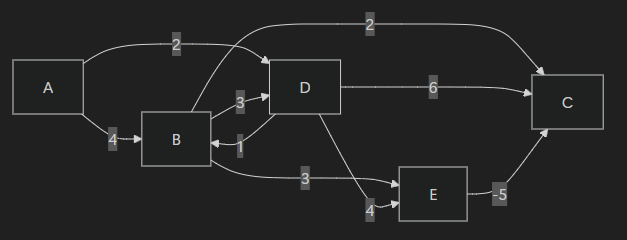
Passo 1:
Semelhante ao algoritmo de Dijkstra, usaremos uma tabela de distâncias para rastrear os caminhos mais curtos. Teremos uma linha para cada iteração e uma coluna para cada vértice.
O número de iterações do Bellman-Ford é igual ao número de vértices menos um:
it = V-1
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1ª It | |||||
| 2ª It | |||||
| 3ª It | |||||
| 4ª It |
Agora escolhemos o vértice de origem. Para este exemplo, vamos definir A como o ponto de partida.
Passo 2
Inicializamos a tabela preenchendo a distância a partir do vértice A para os outros vértices.
A forma de representação será (<Custo>, <Origem>) e, caso o caminho seja impossível, indicamos -.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1ª It | (0, A) | (4, A) | - | (2, A) | - |
| 2ª It | |||||
| 3ª It | |||||
| 4ª It |
Após a primeira iteração, conseguimos chegar até:
- A com o custo 0;
- B com o custo 4;
- D com o custo 2.
Passo 3
Agora aplicamos o relaxamento de arestas baseado nas seguintes regras:
- Se um novo vértice for acessível, somamos o custo da aresta ao custo do vértice anterior.
- Se já acessamos um vértice anteriormente, verificamos se um novo caminho reduz o custo. Caso sim, atualizamos o valor (relaxamento).
- Se nenhum novo caminho foi descoberto, propagamos o custo da iteração anterior.
Exemplo de atualizações:
- B: Um novo caminho é descoberto passando por D → B com custo (2 + 1) = 3. Como 3 é menor que 4, atualizamos o custo.
- D: Já foi alcançado na iteração anterior, então permanece com custo 2.
- C: Pode ser acessado por B → C (4 + 2 = 6) ou D → C (2 + 6 = 8). O menor custo é 6 via B.
- E: Pode ser acessado por B → E (4 + 3 = 7) ou D → E (2 + 4 = 6). O menor custo é 6 via D.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1ª It | (0, A) | (4, A) | - | (2, A) | - |
| 2ª It | (0, A) | (3, D) | (6, B) | (2, A) | (6, D) |
| 3ª It | |||||
| 4ª It |
Passo 4
Nesta iteração, observamos uma nova possibilidade para C:
- C agora pode ser acessado por E → C (6 + (-5) = 1). Como 1 é menor que 6, atualizamos o custo.
- E continua com custo 6, pois não há caminho melhor.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1ª It | (0, A) | (4, A) | - | (2, A) | - |
| 2ª It | (0, A) | (3, D) | (6, B) | (2, A) | (6, D) |
| 3ª It | (0, A) | (3, D) | (1, E) | (2, A) | (6, D) |
| 4ª It |
Passo 5
- Nenhuma nova atualização ocorre.
- Propagamos os valores da terceira iteração.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1ª It | (0, A) | (4, A) | - | (2, A) | - |
| 2ª It | (0, A) | (3, D) | (6, B) | (2, A) | (6, D) |
| 3ª It | (0, A) | (3, D) | (1, E) | (2, A) | (6, D) |
| 4ª It | (0, A) | (3, D) | (1, E) | (2, A) | (6, D) |
Após essa iteração, os menores caminhos foram determinados:
- A → A = 0
- A → B = 3 (A → D → B)
- A → C = 1 (A → D → E → C)
- A → D = 2 (A → D)
- A → E = 6 (A → D → E)
Detecção de Ciclo Negativo
Agora, introduzimos um grafo com ciclo negativo para ilustrar sua detecção.
graph LR
A -->|4| B
A -->|2| D
B -->|2| C
B -->|3| D
B -->|3| E
C -->|4| D
D -->|1| B
D -->|4| E
E -->|-9| C
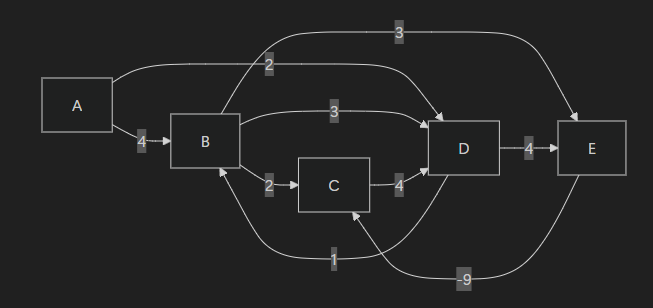
Após V-1 iterações, fazemos uma iteração extra:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1ª It | (0, A) | (4, A) | - | (2, A) | - |
| 2ª It | (0, A) | (3, D) | (6, B) | (2, A) | (6, D) |
| 3ª It | (0, A) | (3, D) | (-3, E) | (2, A) | (6, D) |
| 4ª It | (0, A) | (3, D) | (-3, E) | (1, C) | (6, D) |
| Extra | (0, A) | (2, D) | (-4, E) | (0, C) | (5, D) |
Como há mudança na iteração extra, detectamos um ciclo negativo.
Complexidade Assintótica
A eficiência de um algoritmo é medida pela sua complexidade assintótica, que nos dá uma ideia de seu desempenho conforme o número de vértices (V) e arestas (E) do grafo cresce.
Pior Caso: O(V x E)
- O algoritmo executa o relaxamento de todas as arestas V−1 vezes no pior caso. Como há E arestas, o total de operações será:
O( (V−1) ×E ) = O(V × E)
- Esse pior caso acontece quando o grafo não está otimizado e cada relaxamento melhora uma distância, exigindo todas as iterações.
Desafios e Limitações
- Tempo de Execução: Com complexidade
O(V x E), Bellman-Ford pode ser lento em grafos grandes. - Não é eficiente para grafos sem pesos negativos: O Dijkstra é uma alternativa mais eficiente quando não há pesos negativos.
- Ciclos Negativos podem tornar a solução inválida: Se um ciclo negativo for detectado, o algoritmo informa sua existência, mas não pode calcular caminhos mínimos confiáveis, pois o custo pode ser reduzido indefinidamente.
Possíveis Otimizações
- Encerramento antecipado: Se nenhuma aresta for relaxada em uma iteração, o algoritmo pode ser encerrado antes de completar V-1 iterações.
- Versão otimizada com fila (SPFA - Shortest Path Faster Algorithm): Usa uma fila para processar apenas os vértices que podem ser melhorados, reduzindo o número de relaxamentos.